
As a result, it manages to reduce the complexity of computing the DFT from O ( N 2 ) multiplications by complex roots of unity traditionally called twiddle factors (after Gentleman and Sande, 1966 ). An FFT rapidly computes such transformations by factorizing the DFT matrix into a product of sparse (mostly zero) factors. This operation is useful in many fields, but computing it directly from the definition is often too slow to be practical. The DFT is obtained by decomposing a sequence of values into components of different frequencies. Fourier analysis converts a signal from its original domain (often time or space) to a representation in the frequency domain and vice versa. So we're going to exploreĪll of that in future videos.A discrete Fourier analysis of a sum of cosine waves at 10, 20, 30, 40, and 50 HzĪ fast Fourier transform ( FFT) is an algorithm that computes the discrete Fourier transform (DFT) of a sequence, or its inverse (IDFT). Where we can start doing some signal processing. Going to get us into the frequency domain,
#FOURIER TRANSFORM SERIES#
Series and eventually, Fourier Transforms, that's We have of each frequency? And as we'll see with Fourier Not just in terms of the time domain which f of t does,īut it can start bringing us to saying well, how much do Say, hey, this helps us start to think of a function Two pi hertz frequency than the one over pi frequency. That function contains a lot more of the one over Is much bigger than a two, then that tells you that Of different frequencies that this function contains. These cosines and sines, but another way to think about it is, they tell you how much Used in electrical engineering, is you can view theseĬoefficients as they are, they're weights on

Another really interestingįoundation of signal processing, it's very used, it's heavily Might be able to find more general solutions to Represent that square wave as sums of sines and cosines, then all of a sudden you Obvious to solve when you have more general functions, like When you involve sines and cosines, but not as To him in the study of differential equations,īecause a lot of differential equations are easy to solve Weighted sines and cosines, this was explored originally by Fourier, and they're called Fourier Series. Series where you represent something by essentially Well, okay, this seems like a fun little mathematical exercise, but why do folks even do this? Well this was firstĮxplored, and they're named, series like this, infinite This has a frequency of one over two pi, this has twice the frequency, this has a frequency of one over pi. So let's add a sub two, soĪnother waiting coefficient, times cosine of two t. Is we're gonna add sinusoids of frequencies that are This would look likeĪ very clean sinusoid, not like a square wave. To describe this function, because we know what this would look like. Of cosine of t in it, than it has of sine of t in it. Than b one, well it says, okay, this has a lot more It would make sense that it would involve some functions Has a period of two pi, and I just set up this one so it does have a period of two pi, well Why am I starting withĬosine of t and sine of t? Well, if our original function
#FOURIER TRANSFORM PLUS#
Now, why am I starting with cosine of t? And I could also add a sine of t, so plus b sub one, of sine of t. Then, let's start adding some periodic functions here. Going to be based on the average value of theįunction over one period. That'll shift it up or down, and as we'll see, that's

It's going to be sum, let's say baseline constant,
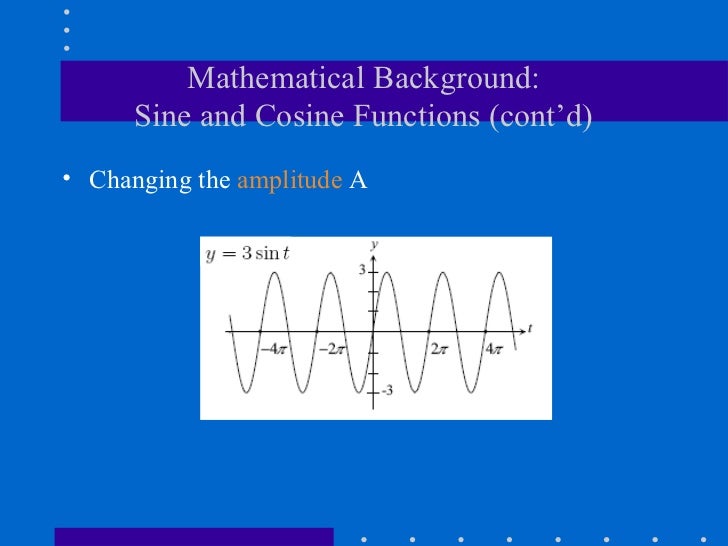
Of sines and cosines? So can we write it, so So can we take our f of t, and write it as the sum Little bit more clearly, can we take our f of t, Sum of sines and cosines of different periods orĭifferent frequencies? So to write that out a And what we're gonnaĮxplore in this video, is can we take a periodicįunction like this and represent it as an infinite So we could write itsįrequency is equal to one over two pi cycles per second,Ĭycles per second, it could also be described as hertz.

We could say two pi, two pi seconds per cycle, Period is equal to two pi, if we wanna put the units It is a periodic function, that it completes oneĬycle every two pi seconds. Is often described as a square wave, and we see that The graph of y is equal to f of t here, our horizontalĪxis is in terms of time, in terms of seconds.


 0 kommentar(er)
0 kommentar(er)
